Algebra 1 Systems Of Equations

A arrangement of linear equation comprises 2 or more linear equations. The solution of a linear system is the ordered pair that is a solution to all equations in the system.

Ane manner of solving a linear system is past graphing. The solution to the system will then exist in the point in which the ii equations intersect.

Example

Solve the following system of linear equations

$$\left\{\brainstorm{matrix} y=2x+4\\ y=3x+2 \cease{matrix}\right.$$

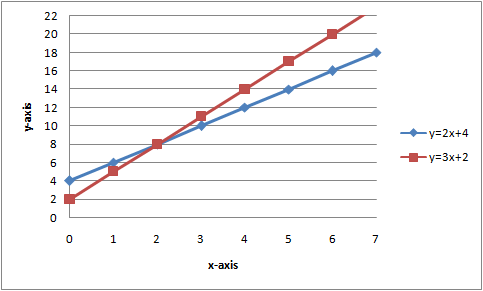
The two lines appear to intersect in (ii, 8)

Information technology's a proficient idea to e'er bank check your graphical solution algebraically by substituting x and y in your equations with the ordered pair

$$\underline{y=2x+iv} \\ {\color{green} eight}\overset{?}{=} two\cdot {\color{green} two}+4$$

$$eight=viii$$

$$\underline{y=3x+two}$$

$${\color{green} eight}\overset{?}{=}3\cdot {\color{green} 2}+2$$

$$8=8$$

A linear organization that has exactly ane solution is called a consistent independent system. Consistent ways that the lines intersect and independent means that the lines are distinct.

Linear systems composes of parallel lines that have the aforementioned slope but different y-intersect practise not have a solution since the lines won't intersect. Linear systems without a solution are called inconsistent systems.

Linear systems composed of lines that accept the same slope and the y-intercept are said to exist consistent dependent systems. Consistent dependent systems take infinitely many solutions since the lines coincide.